信号与系统 chapter 04-05 & 09-10 总结归纳

Review

在上一篇博客中，我们初步的接触了信号与系统，学习了一个简单但是重要的信号：单位冲激信号。对应的，我们学习了在线性时不变系统中如何用单位冲激信号表示一个信号，无论是连续还是离散。以及如果已知单位冲激响应如何求得系统对任何一个信号的响应。由此引入了卷积计算，系统对一个输入信号的响应就等价于输入信号与单位冲激响应做卷积。之后我们通过系统对复指数信号的响应引入了特征函数和特征值的概念，并且表示如果一个信号能够表示为一系列成谐波关系的复指数信号集，那么这个信号就可以写成傅里叶级数，而这样的信号的系统响应很容易求得。

连续时间的傅里叶级数

$ x(t) = \sum_{k=-\infin}^{+\infin}a_{k}e^{jkw_{0}t} = \sum_{k=-\infin}^{+\infin}a_{k}e^{jk(\frac{2\pi}{T})t}, k = 0, 1, 2… $ （综合方程）

$ a_{k} = \frac{1}{T}\int_{0}^{T}x(t)e^{-jkn\omega_{0}t}dt, k \neq 0 $ （分析方程）

离散时间的傅里叶级数

$ x[t] = \sum_{k=(N)}a_{k}e^{jkw_{0}n} = \sum_{k=(N)}a_{k}e^{jk(\frac{2\pi}{N})n}, k = 0, 1, 2… $ （综合方程）

$ a_{k} = \frac{1}{N}\sum_{n=(N)}x(t)e^{-jk(2\pi/N)n}, k \neq 0 $ （分析方程）

以上是两个时间下的傅里叶级数, $ a_{k} $称为傅里叶系数，其表征了信号在频谱中对应频率谐波的分量。

Chapter 04

以连续时间为例，已知$ a_{k} $的表达式，若我们将等式右边的T乘到左边，那么等式右边与周期T无关。如果我们假设周期$ T $无限大，则$ \omega $无限小，等式右边可以看成一个关于$ \omega $的函数。
$$ Ta_{k} = \int_{0}^{T}x(t)e^{-jk\omega t}dt $$

我们称这个表达式为$ Ta_{k} $的包络，记为$ X(j\omega) $。

通过我们刚才的假设可以很容易的得出，连续非周期信号傅里叶变换到频域上表现为一个包络函数。那么连续周期信号实质上是连续非周期信号在时域上卷积脉冲串，进行时域上的搬移。时卷频乘，对应到频域上就是脉冲串乘上包络函数，即对包络函数采样。

于是我们有FT:

$$ Ta_{k} = X(j\omega) = \mathcal{F}{x(t)} = \int_{-\infty}^{\infty}x(t)e^{-j\omega t}dt , \omega = k\omega_{0} $$

一个信号可以表示为傅里叶级数的形式，每一个傅里叶系数都能转换成上述形式，即不同的谐波分量傅里叶变换后的结果不同。

同时，逆傅里叶变化IFT:

$$ x(t) = \mathcal{F}^{-1}{X(j\omega)} = \frac{1}{2\pi}\int_{-\infty}^{\infty} X(j\omega) e^{j\omega t} , d\omega $$

$ \frac{1}{2\pi} $的由来是将傅里叶级数中的$ a_{k} $用包络函数和周期T的关系代替，周期T又可以表示为$ \frac{2\pi}{\omega} $，由此得到。

由于傅里叶变换是在能够表示为傅里叶级数的基础上推演得到的，因此傅里叶变换也需要遵循狄利克雷条件，详见上一篇博客。

那么连续周期信号根据我们上面的分析已知，在频域上是脉冲串的加权和。已知一个频域上出现在$ \omega = \omega_{0} $幅值为$ 2\pi $的脉冲信号$ X(j\omega) = 2\pi \delta(\omega - \omega_{0}) $，通过傅里叶逆变换可以得到其时域表达为$ x(t) = e^{j\omega_{0} t} $。如果是一系列频域上出现在$ \omega = k\omega_{0} $幅值为$ 2\pi a_{k} $的脉冲加权和，通过逆变换后得到在时域上的表示就等于傅里叶级数的表现形式。

由此可以得到，连续周期信号傅里叶变换后频域上表现为出现在成谐波频率点上乘以对应傅里叶系数的$ 2\pi $倍的脉冲加权和。

连续时间傅里叶变换的性质这里不做过多讨论，详细请见下表：

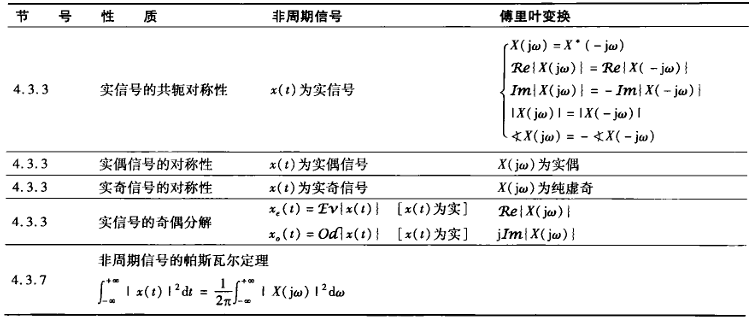
lianxu table

Chapter 05

上一章中主要讲述了连续时间的傅里叶变换，那么离散时间的傅里叶变换是如何推导的呢？

我们已知连续非周期信号傅里叶变换后在频域上表示为一个包络函数，连续周期信号傅里叶变换后在频域上表现为脉冲串对包络函数的采样；

而我们又知道，离散信号就相当于连续信号在时域上乘以脉冲串进行的采样，根据时乘频卷（多了一个$ \frac{1}{2\pi} $的系数）的性质，离散时间的频域表示就等于连续时间的傅里叶变换做了频谱搬移。

由此我们可以发现，离散非周期信号傅里叶变换后频域上表现为周期包络函数，离散周期信号表现为周期包络函数的采样。具体的公式推导如下：

$ DTFT : X(e^{j\omega}) = \sum_{n=-\infty}^{+\infty} x[n] e^{-j\omega n} $

$ IDTFT : x[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(e^{j\omega}) e^{j\omega n} d\omega $

观察DTFT的表达式可以发现，当$ \omega = \omega + 2\pi $时由于n只能为正整数，所以化简后与原式相同。具体来说，离散信号的傅里叶变换是关于频率的周期函数，周期为$ 2\pi $。这是因为离散信号的频谱是连续时间信号频谱的周期性重复。在连续时间信号的傅里叶变换中，频率范围是连续的，但在离散信号的傅里叶变换中，频率范围被限制在$ ((-\pi) - \pi) $之间，然后这个范围内的频谱被周期性地重复。

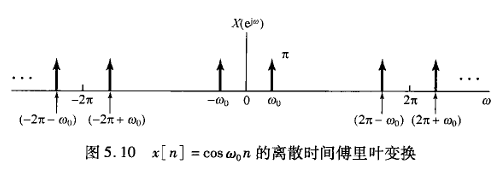
同样的，离散周期信号的傅里叶变换也可以直接由傅里叶系数导出。已知一个周期序列的傅里叶级数为$ x[n] = \sum_{k = N}a_{k}e^{jk(2\pi/N)n} $，那么它的傅里叶变换就直接等于$ X(e^{j\omega}) = \sum_{k=-\infty}^{+\infty}2\pi a_{k}\delta(\omega - \frac{2\pi k}{N}) $，即对周期的包络函数采样，符合我们上面的猜想。例如

lisan example

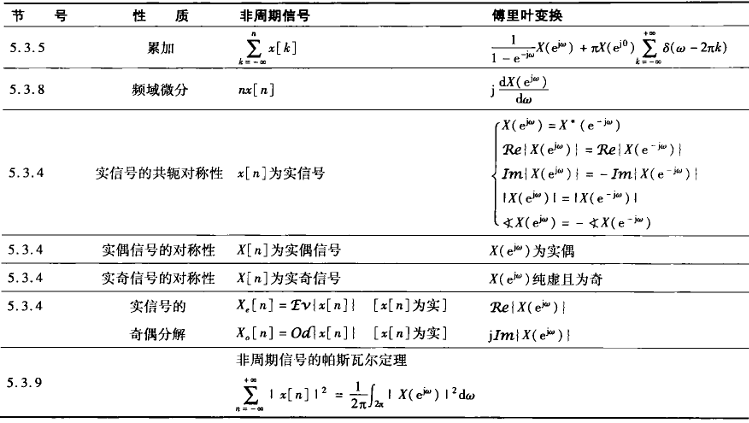
离散时间傅里叶变换的性质详见下图：

lisan table1

lisan table2

lisan table3

lisan table4

以上就是第四、五章的主要内容了，后续我们会对连续时间和离散时间的傅里叶变换做扩展，也就是我们第九、十章的内容，拉普拉斯变换和Z变换。

Chapter 09

在这一章中，我们主要介绍了拉普拉斯变换，它是连续时间信号傅里叶变换的一种推广。我们在Chapter 04中学习了一个单位冲激响应为$ h(t) $线性时不变系统对复指数信号的响应等价于一个特征函数与原复指数信号的乘积。即$ y(t) = H(s)e^{st} $。其中的特征函数为$ H(s) = \int_{-\infty}^{+\infty}h(t)e^{-st}dt $。

前面讨论的复指数信号中的s是纯虚数，那么对于一般的复变量$ s = \sigma + j\omega $来说，$ H(s) $就是单位冲激响应的拉普拉斯变换。我们定义一个信号的拉普拉斯变换为：

$ X(s) = \mathcal{L}{x(t)} = \int_{0}^{\infty}x(t)e^{-st} dt $

当信号的复指数不为纯虚数时，拉普拉斯变换可以表示为：

$ X(\sigma + j\omega) = \mathcal{L}{x(t)} = \int_{0}^{\infty}x(t)e^{-(\sigma + j\omega)t} dt = \int_{0}^{\infty}x(t)e^{-\sigma}e^{-j\omega t} dt $

可以将拉普拉斯变换理解为在输入信号$ x(t) $上增加了一个实指数的增益。这个增益$ e^{-\sigma} $在时间上可以是衰减或者递增的，这取决于$ \sigma $是正还是负。

特殊的，对于两个不同的信号其拉普拉斯变换结果可能相同，只是保证收敛的s的取值范围不同（往往拉普拉斯变换结果相同的两个信号取值范围互补），所以我们给出一个信号的拉普拉斯变换时要将s的取值范围和表达式一起给出。我们称这个s的取值范围为拉普拉斯变换的收敛域，记为$ ROC $。

一个信号可以表示为复指数信号集的形式，那么我们可以单独对每一个复指数信号做拉普拉斯变换，计算其收敛域，最后将所有拉普拉斯变换的结果求和，$ROC$取所有收敛域的交集。只要$x(t)$是实指数或复指数信号的线性组合，那么其拉普拉斯变换$X(s)$一定是有理的，可以表现为$ X(s) = \frac{N(s)}{D(s)} $。而使$N(s)$等于零的s我们称为$X(s)$的零点，同理使$D(s)$等于零的s称为极点。由于拉普拉斯变换的表达式不能确认$X(s)$自身的收敛域，所以说一个有理拉普拉斯变换的完全表征由$X(s)$的零-极点图和收敛域共同构成。

无穷远零点\极点：如果拉普拉斯变换的表达式中分母阶数超过分子阶数k阶，在收敛域内我们说拉普拉斯在无穷远处存在k阶零点；若分子阶数超过分母k阶，在收敛域内我们说拉普拉斯变换在无穷远处存在k阶极点。

已知当$\sigma = 0, s = j\omega$时，拉普拉斯变换就是傅里叶变换，若拉普拉斯变换的收敛域不包括$ j\omega $轴即$ \omega = 0 $则表示该傅里叶变换不收敛。那么拉普拉斯变换的收敛域有什么性质吗？

收敛域的取值只与s的实部有关，即在s平面内是平行与纵轴的带状区域
对有理拉普拉斯变换来说，收敛域内不存在极点（注意无穷远处）
如果输入信号时域上长度有限，且绝对可积则收敛域是整个s平面。解释：可以看成一个有限且可积的信号乘上一个实指数的增益做傅里叶变换，由于满足可积条件则傅里叶变换的结果是一个包络函数，即无穷长度（连续非周期信号）
如果原输入信号是右边信号，且某点在拉普拉斯变换的收敛域内，则该点右边全部的s值都一定在收敛域内。
同理，如果是左边信号，则该点处的左边所有s值都一定在收敛域内。
如果是双边信号，且已知某点在收敛域内，则完整收敛域一定是包含该点的一个带状区域。
如果拉普拉斯变换是有理的，那么其收敛域是被极点界定的或延伸至无穷远处。此外，收敛域内不包含极点。
如果有理，若是右边信号则收敛域在最右边极点的右边；若是左边信号则收敛域在最左边极点的左边。

拉普拉斯逆变换的表达式为：

$ x(t) = \frac{1}{2\pi j}\int_{\sigma - j\omega}^{\sigma + j\omega}X(s)e^{st}ds $

$x(t)$可以用一个复指数信号的加权积分表示，积分路径为s平面内过$ Re{s} = \sigma $的平行于纵轴的一条直线。若拉普拉斯变换有理，则一般将拉普拉斯变换拆分成若干个简单分式，通过固定的变换对反解$x(t)$中的复指数分量，最后加权求和。

拉普拉斯变换的性质表现如下：

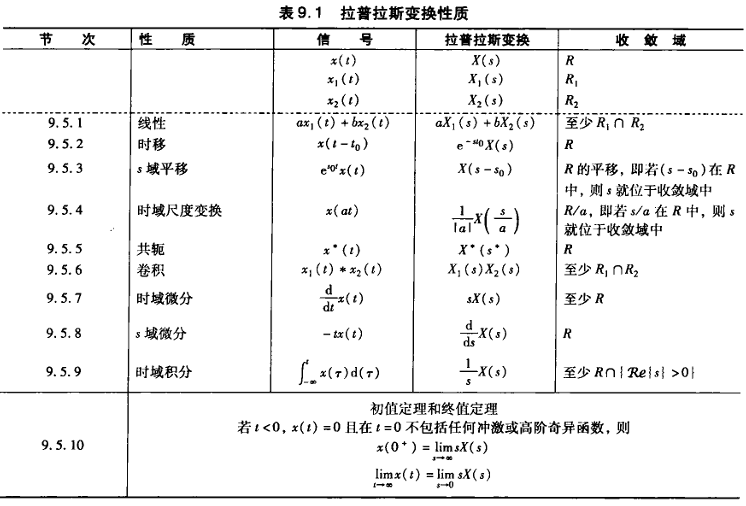
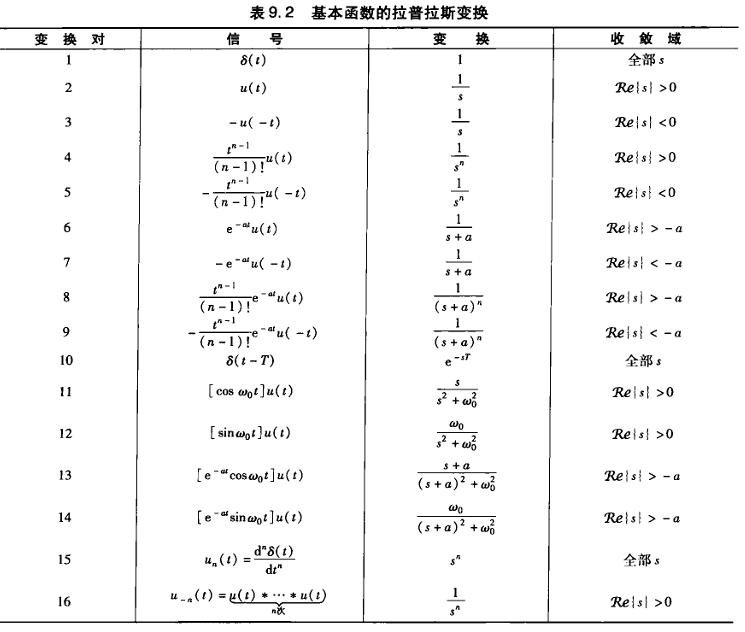
lianxu laplace

如何通过拉普拉斯变换表征线性时不变系统特性

因果性：收敛域是某个右半平面。若是有理拉普拉斯变换，则收敛域是最右边极点的右半平面。
稳定性：当且仅当系统的单位冲激信号的拉普拉斯变换（特征值函数）的收敛域包含S = 0。有理拉普拉斯变换的所有极点都要在s平面的左半平面时一个有理因果系统才稳定。

对于一个用线性常系数微分方程表征的线性时不变系统，他的系统函数为$ H(s) = \frac{Y(s)}{X(s)} $。由拉普拉斯逆变换可以将拉普拉斯变换后的系统函数还原回单位冲激响应。注意！通过线性常系数微分方程获得的系统函数没有收敛域的限制，可若是给出系统因果或者稳定则需要加上收敛域的推演。或者通过对收敛域的判定，可以推导出满足的系统具有的特性如因果、稳定性等。

Chapter 10

对于Z变换的引入与拉普拉斯变换的目的相同，Z变换的性质与拉普拉斯变换的性质十分相似。

$$ X(z) = \sum_{n=-\infty}^{\infty} x[n] z^{-n} $$

以上是Z变换的公式，其中的Z的一般式表现为$ Z = re^{j\omega} $。等效后，Z变换的公式变为：

$$ X(re^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] (re^{j\omega})^{-n} = \sum_{n=-\infty}^{\infty} (x[n]r^{-n})e^{-j\omega n} $$

跟拉普拉斯变换思想一样，对原离散输入信号乘上一个实指数的增益，然后做离散时间的傅里叶变换。在第九章中，我们说当s的实部$\sigma$为零时，拉普拉斯变换就等效于傅里叶变换，这也表明，在复平面内虚轴上的拉普拉斯变换就是傅里叶变换。而对于离散时间的Z变换来说，当Z的模长为一时，Z变换就等效于离散时间的傅里叶变换。在复平面内，我们称这个模长为一的圆为单位圆。由于离散时间傅里叶变换的收敛条件，要求添加增益后的输入信号满足离散傅里叶变换的收敛条件，由此可以得到r即z的模长的取值范围。我们同样称之为$ROC$收敛域。

同样的，Z变换跟拉普拉斯变化一样对于有理的Z变换可以通过零点、极点的分布来判断系统的收敛域。只是拉普拉斯变换的收敛域是复平面内平行于纵轴的条带型区域；而Z变换的收敛域是复平面内以原点为圆心一系列圆，可能圆外、圆内或者圆环。当Z变换的收敛域包含单位圆时，我们可以说该系统稳定，输入信号的离散傅里叶变换收敛。同样的，Z变换的收敛域也有一些性质：

对有理Z变换来说，收敛域内不存在极点（注意无穷远处、原点处）
如果输入信号是有限长序列，则收敛域是整个Z平面，有可能去除原点和无穷远处。
如果输入信号是右边信号，且某半径的圆在Z变换的收敛域内，则半径大于该圆的全部圆都一定在收敛域内。
同理，如果是左边信号，则该圆内部所有半径的圆都一定在收敛域内。
如果是双边信号，且已知某半径的圆在收敛域内，则完整收敛域一定是包含该圆的一个圆环。
如果Z变换是有理的，那么其收敛域是被极点界定的或延伸至无穷远处。此外，收敛域内不包含极点。
如果Z变换是有理的，且原信号是右边序列，则收敛域位于Z平面最外层极点的外边，即半径最大的圆外面；同理左边序列则是最小的圆内部。若因果，则右边序列的Z变化包含无穷远处；左边序列的Z变换收敛域包含原点处。

Z逆变化的表达式如下：

$$x[n] = \frac{1}{2\pi j} \oint_C X(z) z^{n-1} , dz$$

原信号等于在半径为r的Z平面上一个封闭圆沿逆时针绕一圈做积分，这个r可以是收敛域中的任何一个值。与拉普拉斯逆变换相对应，拉普拉斯逆变换是在收敛域的一条纵向直线上做积分，Z逆变换是在收敛域内的一个圆形轨迹上做闭曲线积分。因此，对于有理的Z变换，可以先因式分解为几个简单的分式加权求和，分别做Z逆变换，最终加权求和得到原输入信号。
与之相对应的，每一个分式应该有自己的极点，那么如果$X(z)$的收敛域位于某个分式的极点外侧，则Z逆变换后的对应量系数为正；若收敛域在某个分式的极点内侧，则逆变换后的相应项的系数为负。

对于非有理的Z变换，使用幂级数展开法且Z逆变换十分有效，具体思想就是将Z变换通过长除法等手段写成幂级数（$a_{k}z^{-k}$）的形式，其中当$n > 0$时$a_{k}$就是对应$x[-k]$的值；而当$n < 0$时，$a_{k}$就是对应$x[k]$的值。除此之外还有泰勒级数展开等等，这里不多做描述。

Z变换的性质表现如下：

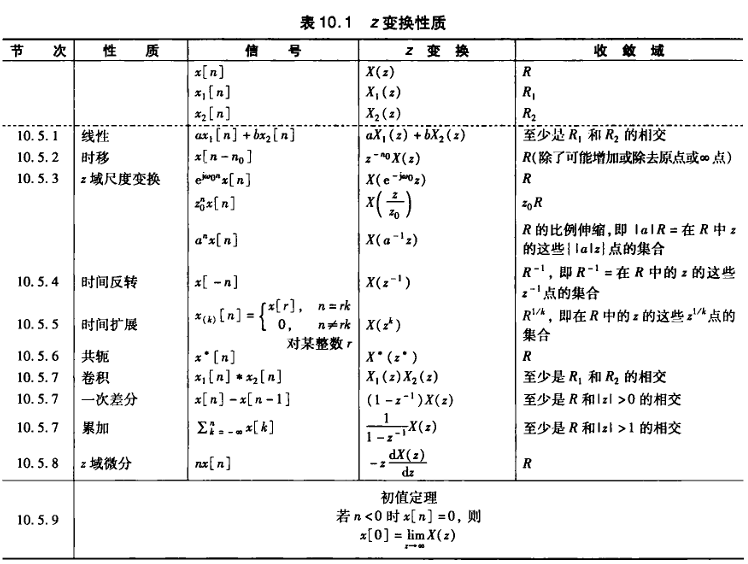
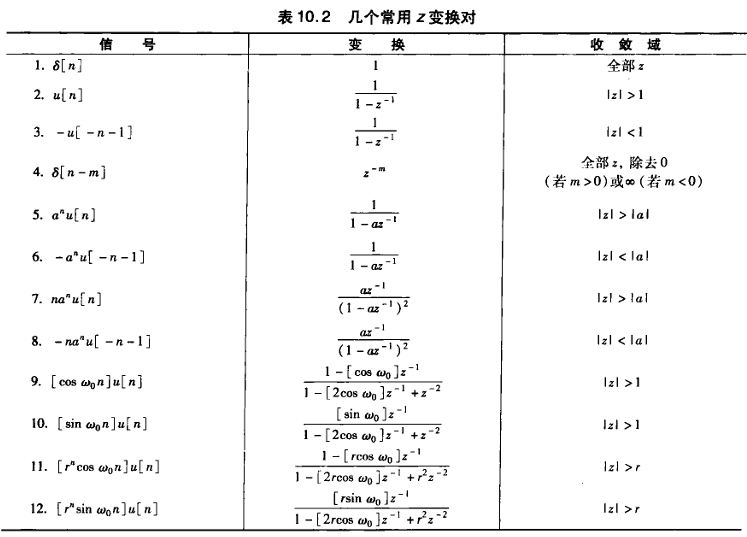
lisan laplace

与拉普拉斯变换相同的，我们可以用Z变化来表征线性时不变系统的特性。如下：

因果性：当且仅当系统的收敛域在某个圆的外边且包括无限远处。若系统还是有理的，则收敛域位于最外层的极点的外边；且若系统函数H()表示为关于s的多项式之比，分子阶数需要低于分母阶数。
稳定性：当且仅当系统的单位冲激响应的Z变换的收敛域包含单位圆。若系统还是有理的，则系统函数的所有极点都需要位于单位圆内，即所有极点的模长都要小于一。

系统框图表示系统函数

对于一个有理的系统函数，我们可以表示为$H(s) = \frac{Y(s)}{X(s)}$，这样我们可以得到y、x之间的关系，无论是变换后的还是原始的。这样我们可以通过系统框图表示该系统。一阶系统一般表示为一个系统框图，高阶的系统可以表现为多个一阶系统之间的级联或者并联。
下面是两个简单的系统框图：

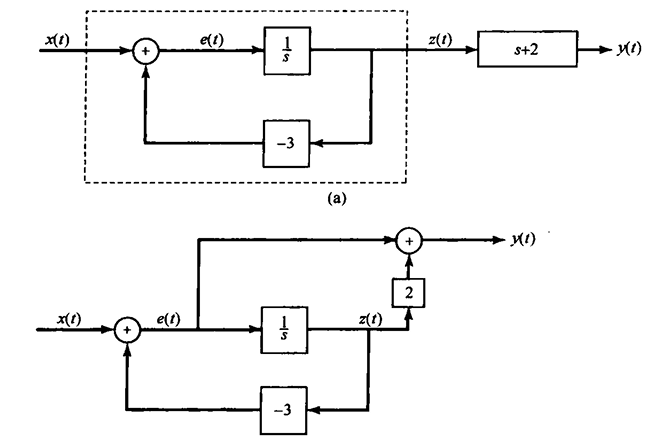
拉普拉斯变换 diagram

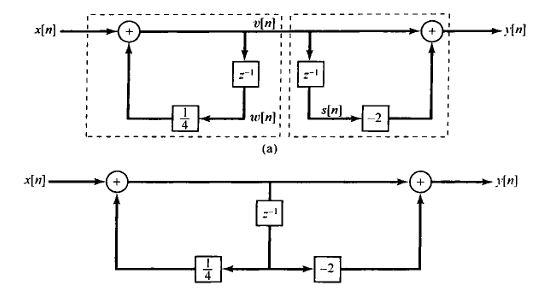
Z变换 diagram

以上就是全部的知识总结了，希望对你有帮助。下一篇就是本书的最后的内容了，我们会开始采样、滤波和信号的调制解调，敬请期待！